Answers

Basic dice duelling

Probability of a draw: 6 out of 36: ⁶⁄₃₆ = ¹⁄₆: ¹⁄₆ × 100 = 16.67%

Excel version of Matrix for Player 1 winning draws

Probability of Player 1 winning: 21 out of 36: ²¹⁄₃₆ = ⁷⁄₁₂: ⁷⁄₁₂ × 100 = 58.33%
Probability of Player 2 winning: 15 out of 36: ¹⁵⁄₃₆ = ⁵⁄₁₂: ⁵⁄₁₂ × 100 = 41.67%

Excel version of matrix for Player 2 having plus 1 and Player 1 wins draws

Probability of Player 1 winning: 15 out of 36: ¹⁵⁄₃₆ = ⁵⁄₁₂: ⁵⁄₁₂ × 100 = 41.67%
Probability of Player 2 winning: 21 out of 36: ²¹⁄₃₆ = ⁷⁄₁₂: ⁷⁄₁₂ × 100 = 58.33%

Changing the dice

Mean average roll on a standard 6-sided die: (1 + 2 + 3 + 4 + 5 + 6) ÷ 6 = 3.5
Mean average roll with the red die: (1 + 4 + 4 + 4 + 4 + 4) ÷ 6 = 3.5
Mean average roll with the green die: (2 + 2 + 2 + 5 + 5 + 5) ÷ 6 = 3.5
Mean average roll with the blue die: (3 + 3 + 3 + 3 + 3 + 6) ÷ 6 = 3.5

Excel version of a matrix for red vs blue

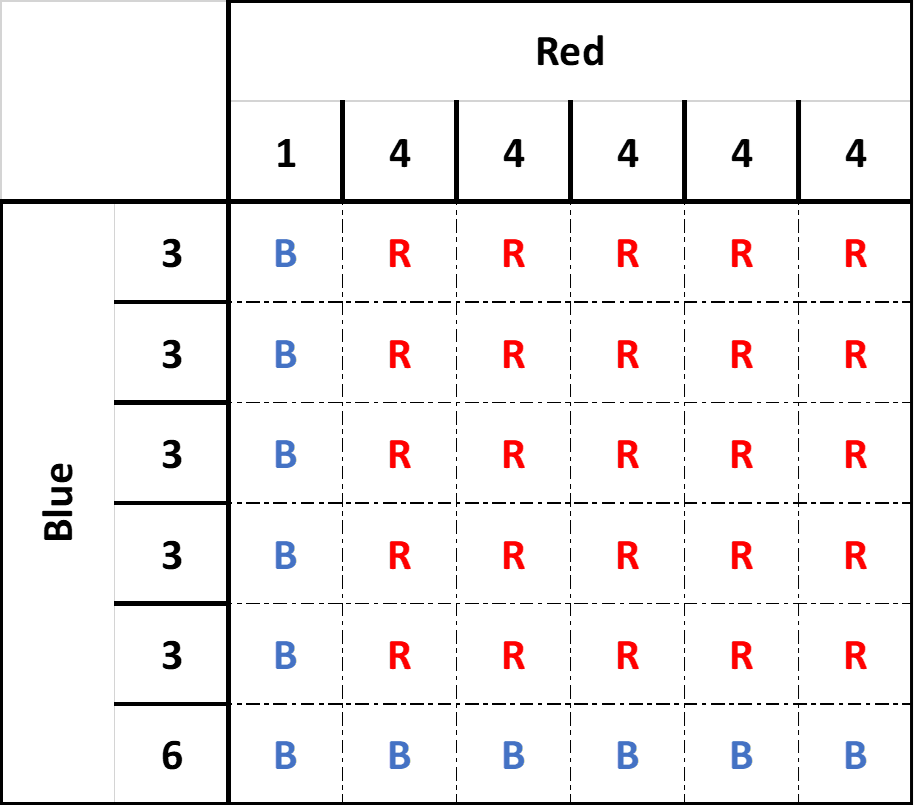
Probability of red winning: 25 out of 36: ²⁵⁄₃₆: ²⁵⁄₃₆ × 100 = 69.44%
Probability of blue winning: 11 out of 36: ¹¹⁄₃₆: ¹¹⁄₃₆ × 100 = 30.56%

Excel version of a matrix for blue vs green

Probability of blue winning: 21 out of 36: ²¹⁄₃₆ = ⁷⁄₁₂: ⁷⁄₁₂ × 100 = 58.33%
Probability of green winning: 15 out of 36: ¹⁵⁄₃₆ = ⁵⁄₁₂: ⁵⁄₁₂ × 100 = 41.67%

Excel version of a matrix for red vs green

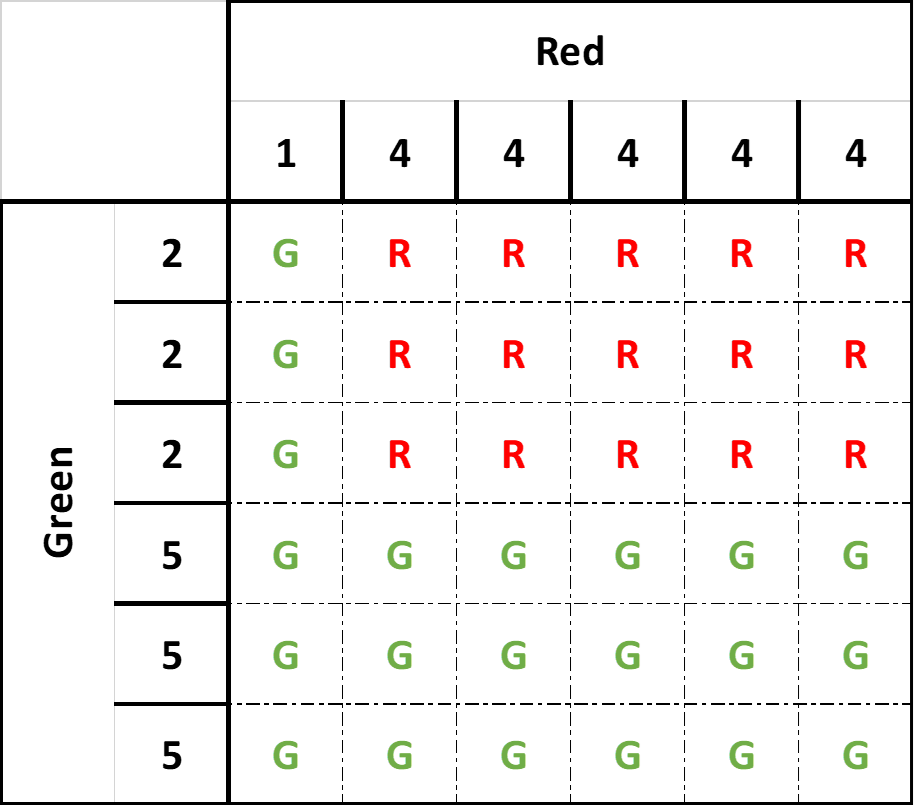
Probability of red winning: 15 out of 36: ¹⁵⁄₃₆ = ⁵⁄₁₂: ⁵⁄₁₂ × 100 = 41.67%
Probability of green winning: 21 out of 36: ²¹⁄₃₆ = ⁷⁄₁₂: ⁷⁄₁₂ × 100 = 58.33%
So, red beats blue, blue beats green, but green beats red. None of the dice are an outright winner.

Back to Workshop