Bridge Design
Imagine two bridges that are exactly alike except that every dimension of one bridge is twice as large as the other. Which of the two bridges would be stronger, or is their strength the same?
How will the volume, and therefore the mass, change?
By multiplying all dimension by two you are causing a volume and mass increase of x8. The larger bridge would therefore collapse under its own weight.
Simple Fractions
If you divide forty by a half and add ten, what is the answer?
Dividing something by a half is the same as doubling it.
40 ÷ ½ + 10 = 90
Birthday Conundrum
The day before yesterday Jasmin was nine years old. Next year she will be twelve. How is this possible?
There is only one day in the year where this can be possible.
It is the 1st January and Jasmin's birthday is on the 31st December. This means she was 9 on the 30th December, 10 on the 31st December, will be eleven at the end of this year and then 12 at the end of next.
No School for Ioan
Ioan explained to his father that he would not be attending school anymore. He said he had been doing some figuring and found that he just didn't have the time for classes. He reasoned, "I sleep eight hours a day and that totals 2,920 hours or 122 days a year. Saturdays and Sundays add up to 104 days a year. If I allow three hours a day for meals, that comes to 45 days a year. The summer holidays add up to 60 days and if I allow just two hours a day for TV and recreation, this amounts to an additional 30 days. If I add all these days, they total 361 and that's not including Christmas, Easter and the other holiday's we get." What is the flaw in Ioan's reasoning?
Look for where times have been counted more than once.
The error in his logic is that he has counted certain activities multiple times. He didn't take into account the fact he'd already counted all meals, recreation and bed times for weekends and the summer holiday before counting them as complete days.
On clearing out her attic, Glenwyn found an old padlocked wooden crate. The lock used on it was a number combination, it needed 4 digits to open. An old, tattered piece of paper was pinned to the lid. It read:
To whomever finds this box.
I, Tobius Flint, have locked away my most treasured possession in this box. Only those that know the year of my birth shall be able to open it.
Yours Sincerely
T.Flint
30th March 1964
(-3,4)(3,-4)(-3,2)(-1,-1)(2,2)(2,4)(1,-4)(-3,-4)(3,4)(-3,0)
(1,4)(2,-4)(-2,-2)(2,-2)(-3,1)(-1,4)(0,-4)(1,-2)(2,0)(-1,0)
(-2,4)(-1,-4)(-1,2)(3,2)(-1,1)(3,0)(-3,-2)(3,-2)(1,0)(-2,2)
(0,4)(-2,-4)(-2,2)(1,2)(-3-1)(-1,-2)
(3,1)(1,-1)(-2,0)
What is the four digit number to unlock this padlock?
Rather than plotting co-ordinates on vertices, try colouring in squares for a clearer picture
By plotting the co-ordinates into squares and colouring them according to the note you should have:
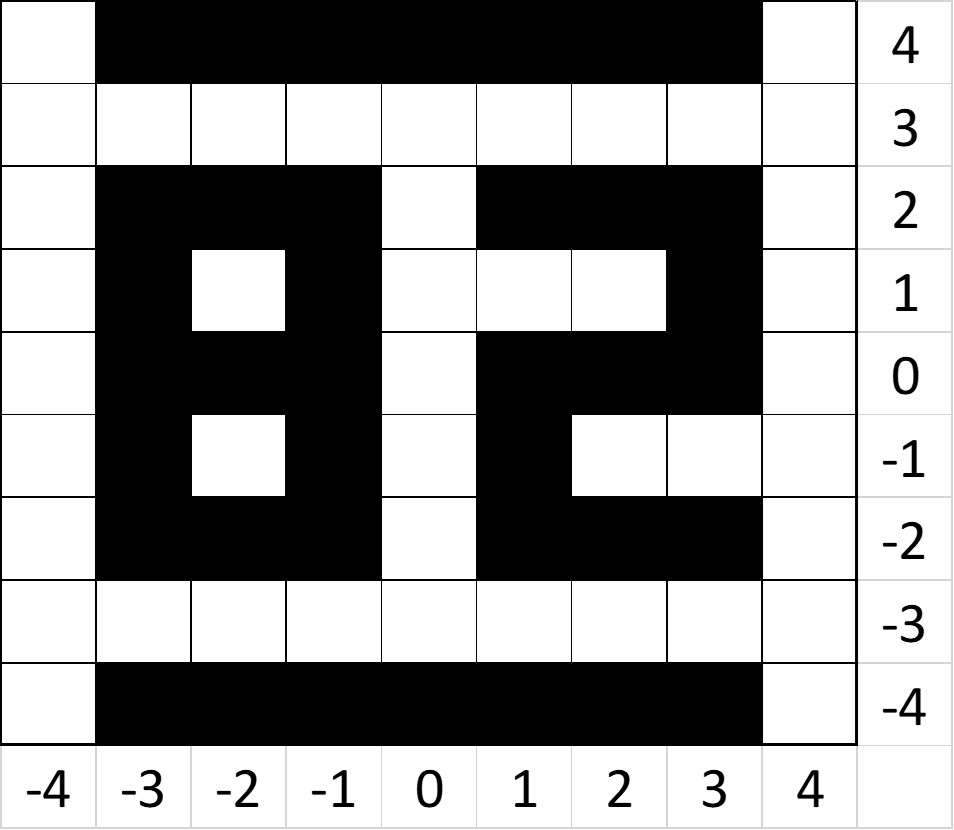
This number could either be the man's age or the last two digits of his date of birth. Using the date on the letter, both approaches will reward you with the answer: 1882.
Draw an 8 by 8 square and cut it into four pieces as shown below. This starting square has area an area of 64 (8 x 8).
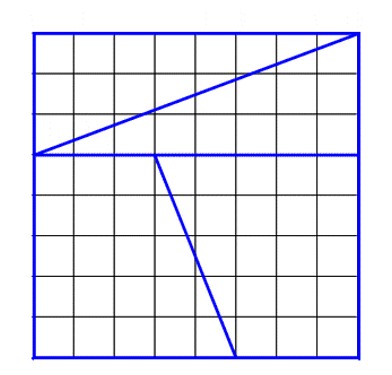
If you rearrange the four pieces, you can build a rectangle whose sides are 13 and 5. This rectangle has an area of 65 (13 x 5). Where did we gain an extra square? That is, how did we gain more area simply by rearranging the pieces.
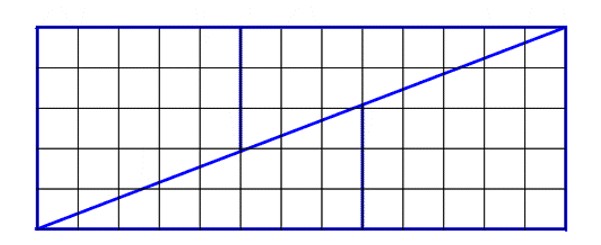
Draw or print out a copy of the square, accurately cut and rearrange to make the rectangle to see how this works.
We know that shapes have a set area no matter their arrangement, so what is happening here? By printing or drawing out the initial square and cutting the shapes as shown, by rearranging physically you can see that the fit is not perfect. There are gaps which seem really small but account for the extra square of area.
A fashionable shirt is manufactured in adult and child versions, 3 different sizes (S,M,L), 10 different colours and comes with 3 different accessories.
Accessories are not necessary, but can be used together in any combination.
How many different choices of shirt and accessories are available?
Number of accessory combinations are 8 (no accessories, one accessory (3 options), two accessories (3 combinations) and all accessories)
Choose either adult or child (2 options)
Choose size (3 options)
Choose colour (10 options)
Choose accessories (8 options) (none, one of three, two of three, or all three)
So total number of combinations = 2 x 3 x 10 x 8 = 480.
For this exercise you will need a sheet of A4 paper and a pair of scissors.
Challenge: Cut a hole in the A4 piece of paper that is large enough for you to step through!
Consider how to cut the paper to make it into a long connected strip.
This is an interesting challenge that may seem impossible at first, until you start thinking of how to make a loop rather than a hole. The image below shows the cut lines for one way to complete this challenge.

The closer together the lines on your paper the larger the loop you can make. It is possible to make a loop big enough to drive a car through, using just A4 paper.
The Earth is 93 million miles from the sun.
This distance is called an Astronomical Unit (AU).
Below is a table of the planets in our solar system, their distance from the sun and the length of their years in Earth time.
| Planet | Distance from the Sun (AU) | Year length in Earth time |
|---|---|---|
| Mercury | 0.39 | 88 days |
| Venus | 0.723 | 225 days |
| Earth | 1 | 365 days |
| Mars | 1.524 | 687 days |
| Jupiter | 5.203 | 11.86 years |
| Saturn | 9.539 | 29.5 years |
| Uranus | 19.18 | 84 years |
| Neptune | 30.06 | 165 years |
Using this information, whilst assuming all orbits are circular, which planet is moving the fastest and which is the slowest?
speed = distance ÷ time.
distance = circumference of orbit = 2πr (where r = distance from the sun)
Using π = 3.14 and year = 365 days
speed (in AU per day) = circumference ÷ time in days
Mercury is the fastest planet travelling at 0.28AU a day.