The Maths of Drawing Hearts

Cymraeg

The Mathematics of Drawing Hearts

This workshop looks at how to draw hearts using various mathematical skills of increasing difficulty.

Click on the title for your chosen level to reveal the challenges, then see how far you can push yourself.

Difficulty Level: Primary

Each of the below challenges require the use of different shapes. We provide the templates for all of these in our Primary Templates pdf


Challenge 1:

Can you produce a heart using these shapes?

A square and two semi-circles. The straight side on each semi-circle is the same length as a side of the square
Hint:

Rotate the square to rest on one point like this:

The square rotated to look like a diamond

Answer:
The square rotated to look like a diamond. The semi-circles and then laid with their straight edges along the top two sides of the diamond. The overall affect is a recognisable heart design

Challenge 2:

Can you produce a heart using these shapes?

Two identical right-angled triangles and two identical semi-circles. The straight edges of the semi-circles are the same length as the shortest side of the triangles

Hint:

Start by matching up the straight side of a semi-circle with a side of the same length on a triangle


Answer:
The semi-circles are each positioned with their straight edge on the matching length side on each triangle. These form the top curves of a heart shape whilst the triangle sides can then be matched up to form an isosceles triangle.

Challenge 3:

Can you produce a heart-like design using these shapes?

A large semi-circle and two identical smaller ones. These smaller ones have a straight edge half the length of the one on the larger semi-circle.

Hint:

Each shape in this challenge only has one straight edge. The straight edges need to rest against each other.


Answer:
The larger semi-circle represents the bottom half of a circle whilst the two smaller rest on top meeting at the mid-point.

Heart Weaving Activity

As a fun additional to this exercise we have included these instructions for how to create your own woven heart designs.

these two templates are made up of a square with a semi-circle attached along the full length of one edge. There is a solid line marking this joining edge. The square is then broken down in 10 columns from the joining edge line to the opposite side of the square with dashed lines.

You can either draw your own version of these shapes or use our printable woven heart templates.

We recommend you use card instead of paper to prevent accidental tearing.

As this activity involves the use of scissors, please make sure there is a responsible adult supervising.

You need to cut the two shapes around the full outline - Do not cut the solid line that goes through the shapes.

Now cut along each of the dashed lines up to the solid line

Carefully weave the strands together, as shown in the below images:

the heart templates after the first blue strand has been woven across the red
the heart templates after the second blue strand has been woven across the red

Once completed it should look something like this:

a completed woven heart design

Tips: You could use paperclips to hold strands in place until completed. You can also use clear tape on the back to hold it all in place

Want to do more? Try out different colours, sizes and numbers of strands.


Difficulty Level: Secondary

These challenges are designed to test your knowledge of shape and line descriptions.

You will need a pencil, ruler, protractor and drawing compass.


Challenge 4:

Follow these instructions:

  1. Draw an isosceles triangle standing on its point. It should be 5cm wide and 7cm tall

    Answer:
    a triangle with parameters to meet this step

  2. Call the points on the horizontal line A (on the left) and B (on the right), whilst the point at its base is C

  3. At point A, draw a 5cm line perpendicular to line AC in the upwards direction.

    Hint:

    What does perpendicular mean?

    To be perpendicular to a line it needs to be at right angles (90°) to it


    Answer:
    a line added to the previous triangle from point A, at a 90° angle to the line AC.

  4. At point B, draw a line perpendicular to line BC, it crosses the line drawn in the previous step at point D

    Answer:
    The triangle formed by adding point D

  5. Using a compass, draw an arc clockwise from point A to D

    Hint:

    What is an arc?

    An arc is a section of a circle's circumference (edge).

    How do I set up the compass for this arc?

    The compass spike should be in the centre of the circle, which will be on the mid-point of line AD.

    The compass should be opened up so as the pencil starts on point A.


    Answer:
    The addition of a semi-circular arc joining points A and D

  6. Using a compass, draw an arc anti-clockwise from point B to D

    Answer:
    The addition of a second semi-circular arc joining points B and D

Challenge 5:

Follow these instructions:

  1. Draw a 5cm horizontal line

  2. Mark one end point A and the other point B

  3. Using point A as the centre, draw a circle with a radius of 2.5cm

    Hint:

    What is the radius of a circle?

    The radius is the distance between the centre of the circle to any point on the arc/circumference.

    Three circles each with a line joining the centre to different parts of the circle's arc/circumference

    Answer:
    A circle with a radius of 2.5cm and a 5cm horizontal line from its centre and out to the right.

  4. Using point B as the centre, draw a circle with a diameter of 5cm

    Hint:

    What is the diameter of a circle?

    The diameter is the distance between opposite points on the arc/circumference of a circle.

    Three circles each with a line joining two different opposite points on their arcs/circumferences

    Answer:
    Two identical circles with their centres at either end of a horizontal line, touching in the middle of the line.

  5. Where the two circles meet, draw a straight line downwards 7 cm. The line end is point C

    Answer:
    Two identical circles with their centres at either end of a horizontal line, touching in the middle of the line. An additional 7cm line goes down vertically from the mid-point of line AB (where the circles meet)

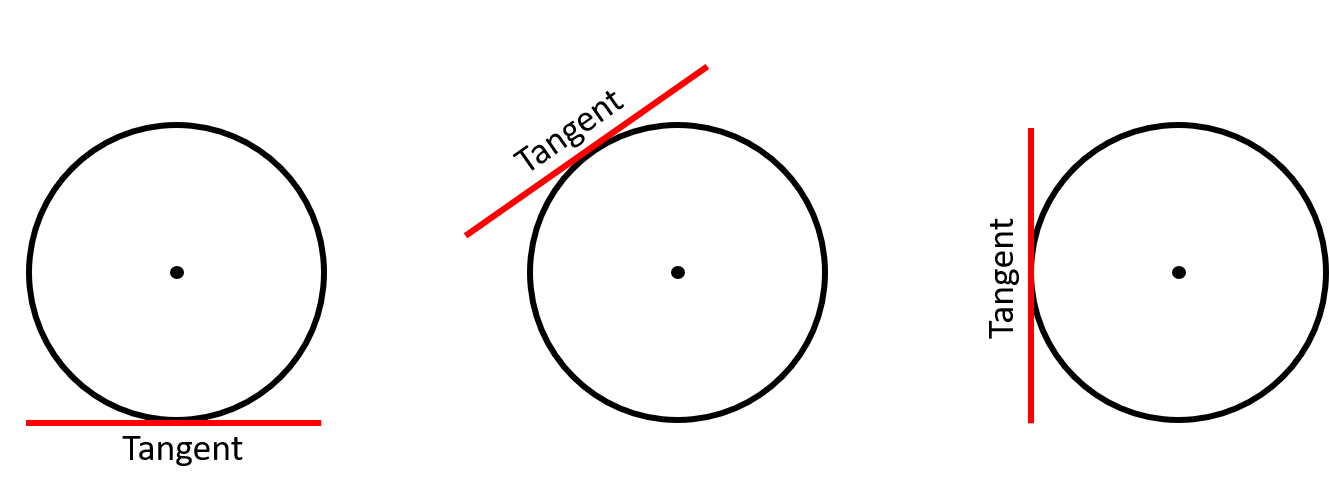
  6. Draw the tangent line for each circle that will connect to point C

    Hint:

    What is a tangent line?

    A tangent to a circle is any straight line that touches on the edge of a circle without passing through the circle's arc.

    Three circles each with a straight line touching a different point on the circle's arc/circumference

    Answer:
    Two identical circles with their centres at either end of a horizontal line, touching in the middle of the line. A 7cm line goes down vertically from the mid-point of line AB (where the circles meet). Two more lines have been added from point C, one to each of the circles and connecting at a tangent

Challenge 6:

Follow these instructions:

  1. Draw a square with an area of 36cm2

    Hint:

    How do I work out the length of the sides?

    The area of any square or rectangle = width x height.

    A square has the same width and height.

    Three squares, the first has sides 1cm in length and therefore has an area of 1cm squared, the second has 2cm sides and therefore has an area of 2 × 2 = 4cm squared, and the third has sides of 3cm and an area = 3 x 3 = 9cm squared

    Answer:
    A square with sides 6cm in length

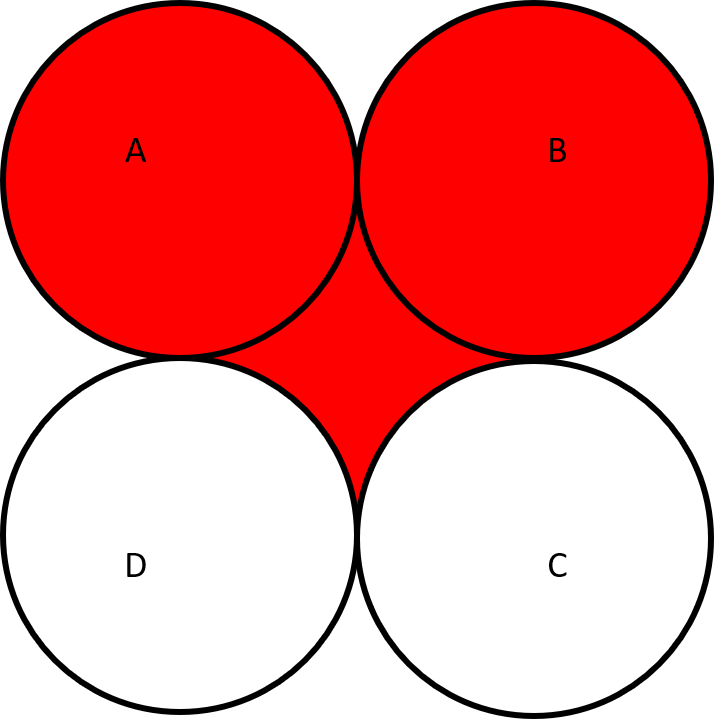
  2. Label the corners A, B, C and D, in a clockwise direction, with A being the top left.

  3. Draw a circle of 6cm diameter with point A as the centre

    Hint:

    What is the diameter of a circle?

    The diameter is the distance between opposite points on the arc/circumference of a circle.

    Three circles each with a line joining two different opposite points on their arcs/circumferences

    Answer:
    A square and circle of equal widths overlaid, with the centre of the circle on the top left corner of the square

  4. Repeat the last step using points B, C and D as the centres

    Answer:
    A square and four circles of equal widths overlaid, with the centre of each circle being on one of the square's corners

  5. Using a red pen/pencil, colour in the circles surrounding points A and B

    Answer:
    The shapes and design from the previous step with the top two circles highlighted

  6. With the same red pen/pencil colour in the shape formed inside the square by the arcs of all four circles

    Answer:
    The same shapes and design as for the previous step with the shape formed inside the square by the arcs of the four different circles also highlighted - all these highlighted areas now produce a variation on the heart design

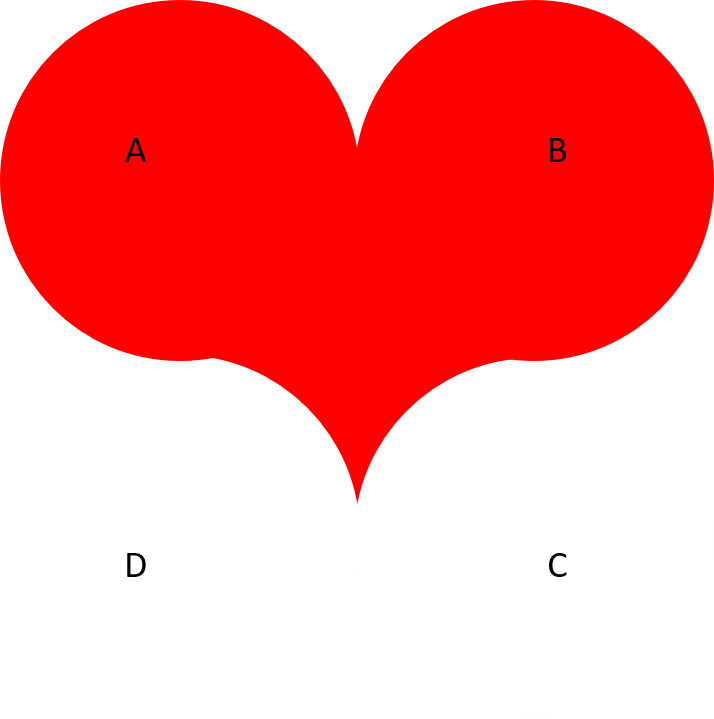
    To help show the final heart design, we have deleted the shape outlines in the below version:

    The above design but with the outlines of the square and the bottom two circles erased, leaving us with just the heart shape


This next selection of challenges will require the use of scissors, glue and tape.

Challenge 7:

  1. Get an A4 piece of paper or card.

  2. Cut off a strip 2cm in width.

  3. Using this single strip of paper (which has two sides), try to create a single-sided shape.

You will not need to use scissors, but you will need some tape.

Hint:

Surely this is impossible? The paper will always have two sides.

It is possible. There is a 'twist' to this challenge when taping the ends together.


Answer:

To create a one-sided shape, tape the paper into a loop with a single twist. To test it, take a pen or pencil and draw a line along the centre of the strip - it should join together without being removed from the paper, proving it is one-sided.

A strip of card with its ends taped together to form a loop with a single twist in it

Challenge 8:

This single-sided shape is called a Möbius Strip.

  1. Either create a new Möbius Strip or use the one from challenge 7, draw a line down the centre.

    Reveal Image
    A strip of card with its ends taped together to form a loop with a single twist in it. A line has been marked along the centre of the strip.

  2. What shape(s) would we get if we cut along this line? Consider this, don't do it yet.

  3. Think about (or even experiment with) what would happen if you cut a simple loop (no twists) of paper along the centre line.

  4. Let us find us out. Cut your Möbius Strip along the centre line.

  5. What shape(s) have you ended up with? How many sides?

    Answer:

    We now have a loop with two sides (an inside and an outside edge) which has four twists!

    A larger loop with 4 twists

  6. How many twists are there in the shape(s)? You can check by cutting through the strip and counting how many times you need to turn the paper to untwist it.

Challenge 9:

  1. Get two new strips of card or paper of the same size and glue them together in a cross.

    Reveal Image
    Two strips of card glued at their centres to form a cross

  2. Tape one of these strips into a simple loop, the other as a Möbius Strip.

    Reveal Image
    A simple loop of black card attached at right-angles to a Möbius Strip.

  3. Cut along the central line of both, not including the joining section.

    Reveal Image
    A simple loop of black card attached at right-angles to a Möbius Strip. Both have been cut along the strips' centre lines round from and to where they are joined.

  4. Before we complete the cuts across the glued section, think about what shape(s) you think this action will create.

    We already know from the previous challenge what happened with just a Möbius Strip, and we know that a single simple loop cut along the centre line will produce two loops.

  5. When you're ready to check your predictions/thoughts, complete the cuts through the last section - you will need to hold them in place between the two cuts.

    Answer:

    We now have a square!

    A square frame of card strips

Was this what you expected?

Challenge 10:

  1. With two new strips of paper/card, glue them together in the same cross configuration as step 1 of challenge 9

  2. This time we will tape them both as Möbius Strips with opposite twists. This means one will be twisted clockwise before taping, the other anti-clockwise.

    Reveal Image
    Two Möbius Strips of identical length and opposite twist directions attached at right angles to each other.

  3. Cut along the central lines of each strip, up to the sides of, but not through, the joining section

    Reveal Image
    Two Möbius Strips of identical length and opposite twist directions attached at right angles to each other. Both have been cut along the strips' centre lines round from and to where they are joined.

  4. Before we complete both the central cuts through the joining section, let's consider what we think might happen this time.

  5. Once you are ready, complete the cuts to see how accurate your predictions were.

    Answer:

    We now have two interlocked hearts.

    Two interlocked heart shapes

Tip: If you ended up with two separated shapes at this point it means the two Möbius Strips were twisted in the same direction, not opposite (as instructed in step 2).


Difficulty Level: A-Level

Challenge 11:

Follow the instructions below:

  1. Draw the graph of \[f(x) = \sin(x)\] for \[0 < x <{\pi \over 2}\]

    Answer:
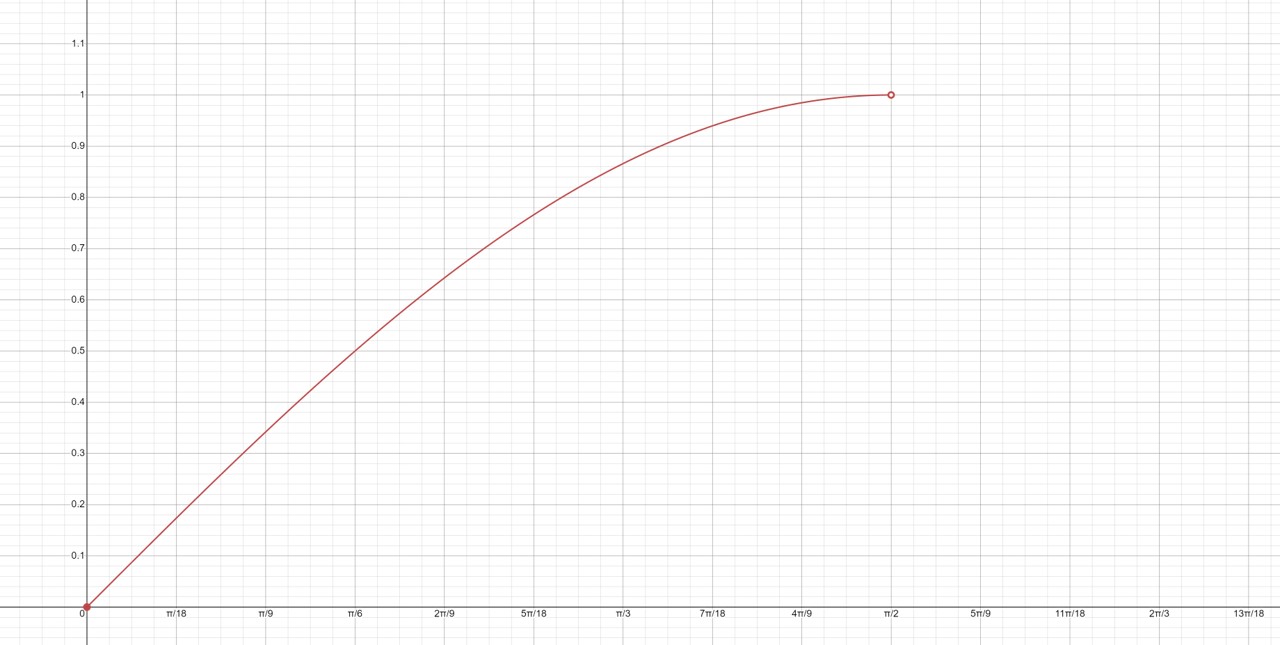
    The graph for the above equation.

    Graph produced using a problem-solving tool available on Mathway.com

  2. Rotate the curve produced by -90°

  3. Draw the reflection of this curve, touching at the base

  4. Draw a horizontal line across the top to form a triangle with two curves and a straight side.

    Answer:
    A triangle made up of the above graph line, it's mirror image and a horizontal line

  5. Mark the left end of this horizontal line point A, the right end as point B and the mid-point as C

  6. Draw a 180° arc joining point A to C in a clockwise direction, repeat to join point C to B

    Answer:
    A combination of the above to form a shape recognisable as a heart symbol

Challenge 12:

Follow the instructions below:

  1. Draw the graph of \[f(x) = \sin(x)\] for \[-{\pi \over 2} < x < {\pi \over 2}\]

    Answer:
    The graph for the above equation.

    Graph produced using a problem-solving tool available on Mathway.com

  2. Rotate the curve produced by -90°

  3. Draw the reflection of this curve, touching at the base

  4. Draw a horizontal line across the top to form a triangle with two curves and a straight side.

  5. Mark the left end of this horizontal line point A, the right end as point B and the mid-point as C

  6. Draw a 180° arc joining point A to C in a clockwise direction, repeat to join point C to B

    Answer:
    A combination of the above to form a shape recognisable as a heart symbol

Challenge 13:

Follow the instructions below:

  1. Draw a graph using the parametric equations \[x = \alpha \cos t (1 - \cos t)\] and \[y = \alpha \sin t (1 - \cos t)\]

  2. Rotate the curve produced by -90°

    Answer:
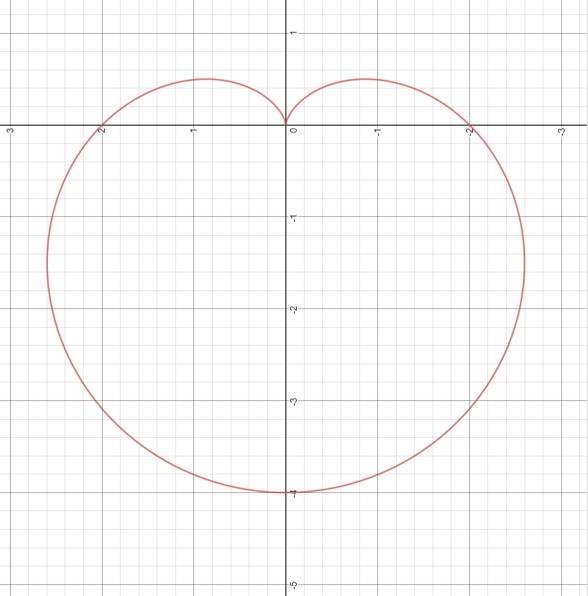
    A cardioid - or a very curved representation of a heart.

    This graph was produced on the Desmos.com Calculator using the polar equation for this curve

This shape is called a cardioid (cardio from the Greek for 'of the heart'). It is more curved then our normal heart designs.

Cardioids can be created naturally, for example through the reflection of light in a circle.

The cardioid is also the main figure of the Mandelbrot set.


Extension Activity

We have another romantic themed workshop online called Turtle Flowers aimed at drawing flowers through programming instructions.

Try to use this same program to accurately reproduce all the heart designs you created here.


Additional Resources

If you are interested in learning more about the mathematics behind hearts, please check out the following websites: