

In this investiagtion we shall be looking at how changing dice alters probabilities.
To start with you will need to have a look at the dragon racing game from the KS2 activity. Feel free to make your own version as some people work better with a real-world application to try it on
If we were to play the dragon racing game or any game of chance involving the use of a single 12-sided dice, there is the equal chance or probability of rolling any number. This means that we would not be able to mathematically predict the winning value. If you want to give this a try, here is the template for a 12-sided die to make, if you don't have access to one.
The probability of any number being rolled can be written as 1 in 12 or 1⁄12. We can also calculate the percentage chance using 1 ÷ 12 × 100 (remember you always do division before multiplication). So you have a 8.33% chance of rolling a 1, 8.33% chance of rolling a 2, etc.
Using probability we can predict which numbers are most likely to win in a race. By replacing a single 12-sided die with two 6-sided dice we have changed the possibilities. Firstly we have made it impossible to roll a 1 so we know not to back that dragon. What other effects has this change made?
If you haven't already I would advise you 'play' the dragon racing game a few times, using the blank results table provided, boardgame, or by mentally recording your dice rolls. Here is a 6-sided dice template if you cannot find any
When we used a single 12-sided die there were only 12 possible outcomes. Each time you rolled the die, you were going to get a value between 1 and 12 everytime. With two 6-sided dice the total is now limited to any number between 2 and 12, however, the number of combinations of dice values has increased. How can we calculate how many different dice combinations there are? We could write them down and then add up how many there are;
This could take a while, and if you miss a combination, your total will be wrong and any probability calculations you do later will be incorrect. Another method would be to produce a matrix:

Now we can see all possible dice rolls and easily determine there are 36 different combinations. We can also see that more combinations add up to 7 than any other number. This means we mathematically know that the number 7 dragon will win more often. Now, if we ignore the race and just focus on the dice rolls, what is the probability, in the form of fractions and percentages, of rolling each number?
Let me give an example to set you on the way: The probability of rolling a total of 5 is 4 in 36. This is the number of combinations that equal 5 in the matrix out of the total number of possible combinations. As a fraction we could write 4⁄36. However, we should always write a fraction in it's simplest form, in this case 4⁄36 = 1⁄9. Here is the link to an external website that explains about simplifying fractions if you need a reminder or have not yet covered this in class. As a percentage this would then be 1 ÷ 9 × 100 = 11.11%. This means we are more likely to roll a total of 5 on two 6-sided dice than we are on a 12-sided die.
We have now seen the effect of changing from one 12-sided die to two 6-sided dice on probability. What if we could use a combination of two different dice that add up to 12? Would this alter the chances of certain totals being rolled? Let's find out.
Let us imagine we have a 5-sided and a 7-sided dice. The maximum total is still 12, but how many combinations are there? You will need to draw a new matrix to work out how many combinations and there totals are.
Once you've completed the matrix, calculate the probabilities for each number between 2 and 12 being rolled in both fraction and percentage form.
Now do the same; a matrix and probability calculations, for using a 4-sided with an 8-sided dice.
There is one instantly noticeable issue with using three dice; we now can no longer roll a 1 or a 2. A mathematical issue is that we cannot use a single matrix to demonstrate the different combinations. We can however determine how many combinations there are. Looking back at your previous matrices you can see that when we had two 6-sided dice there were 36 combinations; a 5-sided and a 7-sided dice has 35 combinations; and the 4-sided and 8-sided dice has 32. Can you see the pattern?
If we multiply the total number of sides of each dice together we get the total number of possible combinations. So to calculate the number for three 4-sided dice we need to do 4 × 4 × 4 = 64 combinations!
We could display all this different combinations across four matrices with the first having an extra 1 added to each total to represent a roll of one on the third dice, the second has +2, the third +3 and the fourth +4 as shown below:
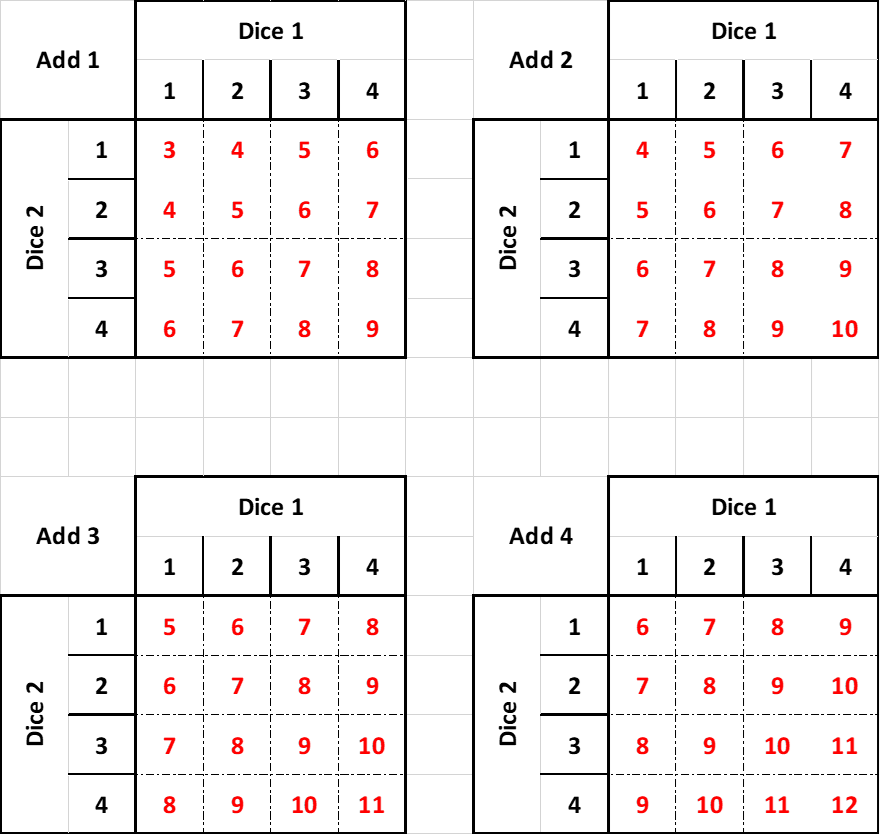
Now you've been provided with the matrices you can calculate the probabilies of each total being rolled as both a fraction and a percentage
Finally, it is time for you to implement all the above methodology and calculate the percentage probabilities for each possible roll total when using the combination of a 3-sided, a 4-sided and a 5-sided dice.
How would you investigate and calculate the possibilities involved if we were to use four 3-sided dice? Give it a go.
So which dice combination is best for each of the dragons in the race?
Here is a link to the answers page. In it are provided all the answers with workings. Please only use if you have finished all the sections you can or are completely stuck.