Ymchwilio i Gyfuniadau Deis Gwahanol
Yn yr ymchwiliad hwn byddwn yn edrych ar sut mae newid dis yn newid tebygolrwydd.
I ddechrau, bydd angen i chi edrych ar y gêm rasio'r ddraig o weithgaredd CA2. Mae croeso i chi wneud eich fersiwn eich hun gan fod rhai pobl yn gweithio'n well drwy ei chymhwyso i'r byd go iawn i roi cynnig arni.
Dis 12-ochrog
Pe baem yn chwarae gêm rasio'r ddraig neu unrhyw gêm siawns sy'n cynnwys defnyddio un dis 12-ochrog, mae siawns neu debygolrwydd cyfartal o rolio unrhyw rif. Mae hyn yn golygu na fyddem yn gallu rhagfynegi'r gwerth buddugol yn fathemategol. Os ydych chi am roi cynnig arni, dyma'r templed ar gyfer deis 12-ochrog i'w wneud, os nad oes gennych fodd o gael gafael ar un.
Gellir ysgrifennu tebygolrwydd unrhyw rif yn cael ei rolio fel 1 mewn 12 neu 1⁄12. Gallwn hefyd gyfrifo'r siawns fel canran drwy ddefnyddio 1 wedi'i rannu â 12 wedi'i luosi â 100 (cofiwch eich bod bob amser yn rhannu cyn lluosi). Felly, mae gennych siawns o 8.33% o rolio siawns 1, 8.33% o rolio 2, ac ati.
Defnyddio dau ddis 6-ochrog
Gan ddefnyddio tebygolrwydd, gallwn ragweld pa rifau sydd fwyaf tebygol o ennill mewn ras. Trwy gael dau ddis 6-ochrog yr un yn lle'r un dis 12-ochrog rydym wedi newid y posibiliadau. Yn gyntaf, rydym wedi ei gwneud yn amhosibl rholio 1 felly rydym yn gwybod i beidio â chefnogi'r ddraig honno. Pa effeithiau eraill sy'n dod yn sgil y newid hwn?
Os nad ydych wedi gwneud hynny eisoes, byddwn yn eich cynghori i 'chwarae' y gêm rasio'r ddraig ychydig o weithiau, gan ddefnyddio'r tabl canlyniadau gwag a ddarperir, bwrdd chwarae, neu trwy recordio rholiau eich dis yn eich meddwl. Dyma dempled dis 6-ochrog os na allwch ddod o hyd i rai.
Wrth ddefnyddio un dis 12-ochrog, dim ond 12 canlyniad posib oedd yna. Bob tro roeddech chi'n rholio'r dis, roeddech chi'n mynd i gael gwerth rhwng 1 a 12 bob tro. Gyda dau ddis 6-ochrog mae'r cyfanswm bellach wedi'i gyfyngu i unrhyw rif rhwng 2 a 12, fodd bynnag, mae nifer y cyfuniadau o werthoedd dis wedi cynyddu. Sut gallwn ni gyfrifo faint o gyfuniadau dis sydd yna? Gallem eu hysgrifennu i lawr ac yna adio faint sydd yna:
5 + 4 = 9
2 + 1 = 3
6 + 3 = 9
etc...
Byddai hyn yn gallu cymryd cryn amser, ac os byddwch chi'n colli cyfuniad, bydd eich cyfanswm yn anghywir a bydd unrhyw gyfrifiadau tebygolrwydd a wnewch yn ddiweddarach yn anghywir. Dull arall fyddai llunio matrics:

Fersiwn Excel o fatrics dau ddis 6-ochrog ar gyfer darllenwyr sgrin
Nawr gallwn weld yr holl roliau dis posib a phenderfynu'n rhwydd bod yna 36 cyfuniad gwahanol. Gallwn hefyd weld bod mwy o gyfuniadau yn adio i 7 nag unrhyw rif arall. Mae hyn yn golygu ein bod ni'n gwybod yn fathemategol y bydd y ddraig rhif 7 yn ennill yn amlach. Nawr, os ydym yn anwybyddu'r ras a dim ond yn canolbwyntio ar y rholiau dis, beth yw'r tebygolrwydd, ar ffurf ffracsiynau a chanrannau, o rolio pob rhif?
Gadewch imi roi enghraifft i'ch gosod ar y ffordd: Y tebygolrwydd o rolio cyfanswm o 5 yw 4 mewn 36. Dyma nifer y cyfuniadau sy'n hafal i 5 yn y matrics allan o gyfanswm nifer yr holl gyfuniadau posibl. Fel ffracsiwn gallem ysgrifennu 4⁄36. Fodd bynnag, dylem bob amser ysgrifennu ffracsiwn yn ei ffurf symlaf, yn yr achos hwn 4⁄36 = 1⁄9. Dyma'r ddolen i wefan allanol sy'n egluro symleiddio ffracsiynau os oes angen nodyn atgoffa arnoch neu os nad ydych wedi astudio hyn yn y dosbarth eto. Fel canran, byddai hyn wedyn yn 1 ÷ 9 × 100 = 11.11%. Mae hyn yn golygu ein bod yn fwy tebygol o rolio cyfanswm o 5 ar ddau ddis 6-ochrog nag yr ydym ar ddis 12-ochrog.
Defnyddio dis anarferol
Rydym bellach wedi gweld effaith newid o un dis 12-ochrog i ddau ddis 6-ochrog ar debygolrwydd. Beth pe gallem ddefnyddio cyfuniad o ddau ddis gwahanol sy'n adio i 12? A fyddai hyn yn newid y siawns o rolio ambell i gyfanswm? Dewch i ni weld.
Gadewch inni ddychmygu bod gennym ddis 5-ochrog a dis 7-ochrog. Y cyfanswm uchaf yn dal yw 12, ond faint o gyfuniadau sydd? Bydd angen i chi lunio matrics newydd i ddarganfod faint o gyfuniadau a sawl cyfanswm sydd yna.
Ar ôl i chi gwblhau'r matrics, cyfrifwch y tebygolrwydd i bob rhif rhwng 2 a 12 gael eu rholio, a hynny ar ffurf ffracsiwn a chanran.
Nawr gwnewch yr un peth; cyfrifiad matrics a thebygolrwydd, ar gyfer defnyddio dis 4-ochrog gyda dis 8-ochrog.
Defnyddio tri dis 4-ochrog
Mae un broblem amlwg i'w weld yn syth wrth ddefnyddio tri dis; dydyn ni ddim bellach yn gallu rolio 1 neu 2. Problem fathemategol yw na allwn ddefnyddio un matrics i arddangos y gwahanol gyfuniadau. Fodd bynnag, gallwn benderfynu faint o gyfuniadau sydd. Wrth edrych yn ôl ar eich matricsau blaenorol gallwch weld pan oedd gennym ddau ddis 6-ochrog roedd 36 cyfuniad; mae gan ddis 5-ochrog a dis 7-ochrog 35 cyfuniad; ac mae gan y dis 4-ochrog ac 8-ochrog 32. A allwch chi weld y patrwm?
Os ydym yn lluosi cyfanswm ochrogau pob dis gyda'i gilydd, rydym yn cael cyfanswm y cyfuniadau posibl. Felly, i gyfrifo ar gyfer tri dis 4-ochrog mae angen i ni wneud 4 × 4 × 4 = 64 cyfuniad!
Gallem arddangos yr holl gyfuniadau gwahanol hyn ar draws pedwar matrics, gyda'r cyntaf yn cael 1 ychwanegol wedi'i ychwanegu at bob cyfanswm i gynrychioli rolio un ar y trydydd dis, mae gan yr ail +2, y trydydd +3 a'r pedwerydd +4 fel y dangosir isod:
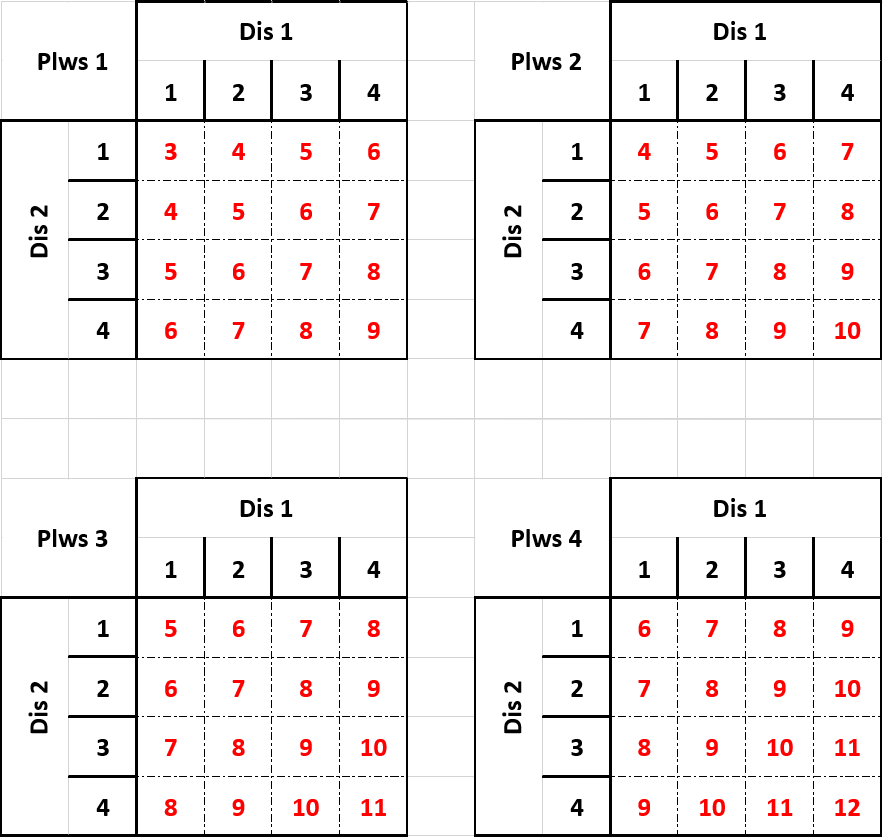
Fersiwn Excel o matrics dri dis 4-ochrog ar gyfer darllenwyr sgrin
Nawr eich bod wedi cael y matricsau gallwch gyfrifo tebygolrwydd pob cyfanswm sy'n cael ei rolio fel ffracsiwn a chanran.
Defnyddio tri dis gwahanol
Yn olaf, mae'n bryd ichi roi'r holl fethodoleg uchod ar waith, a chyfrifo'r tebygolrwyddau mewn canran ar gyfer pob cyfanswm rholio posibl wrth ddefnyddio'r cyfuniad o ddis 3-ochrog, dis 4-ochrog a dis 5-ochrog.
Estyniad
Sut fyddech chi'n ymchwilio ac yn cyfrifo'r posibiliadau pe byddem yn defnyddio pedwar dis 3-ochrog? Rhowch gynnig arni.
Felly pa gyfuniad dis sydd orau ar gyfer pob un o'r dreigiau yn y ras?
Atebion
Dyma ddolen i'r dudalen atebion. Ynddo mae'r holl atebion wrth gyfrifo'r gwaith. Peidiwch â'i ddefnyddio nes eich bod wedi gorffen yr holl adrannau y gallwch eu gwneud neu os ydych yn hollol sownd.