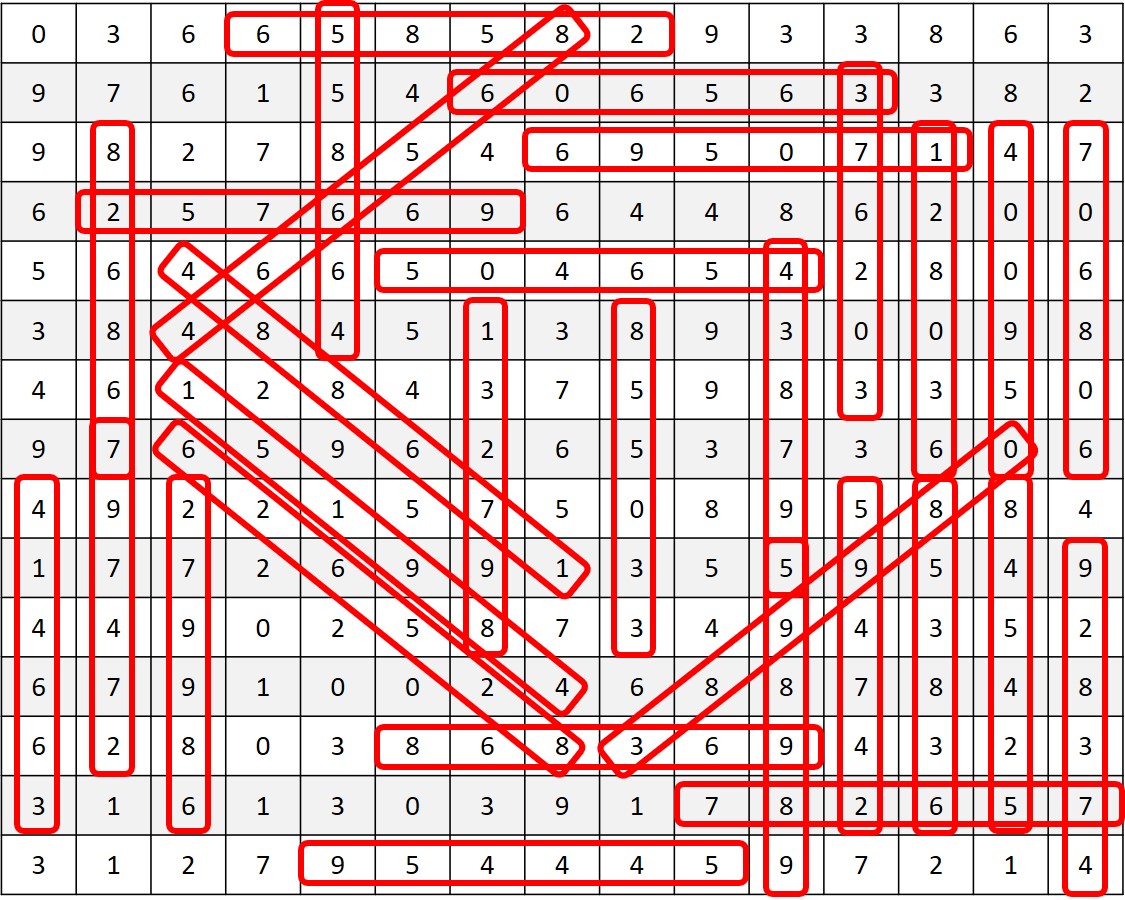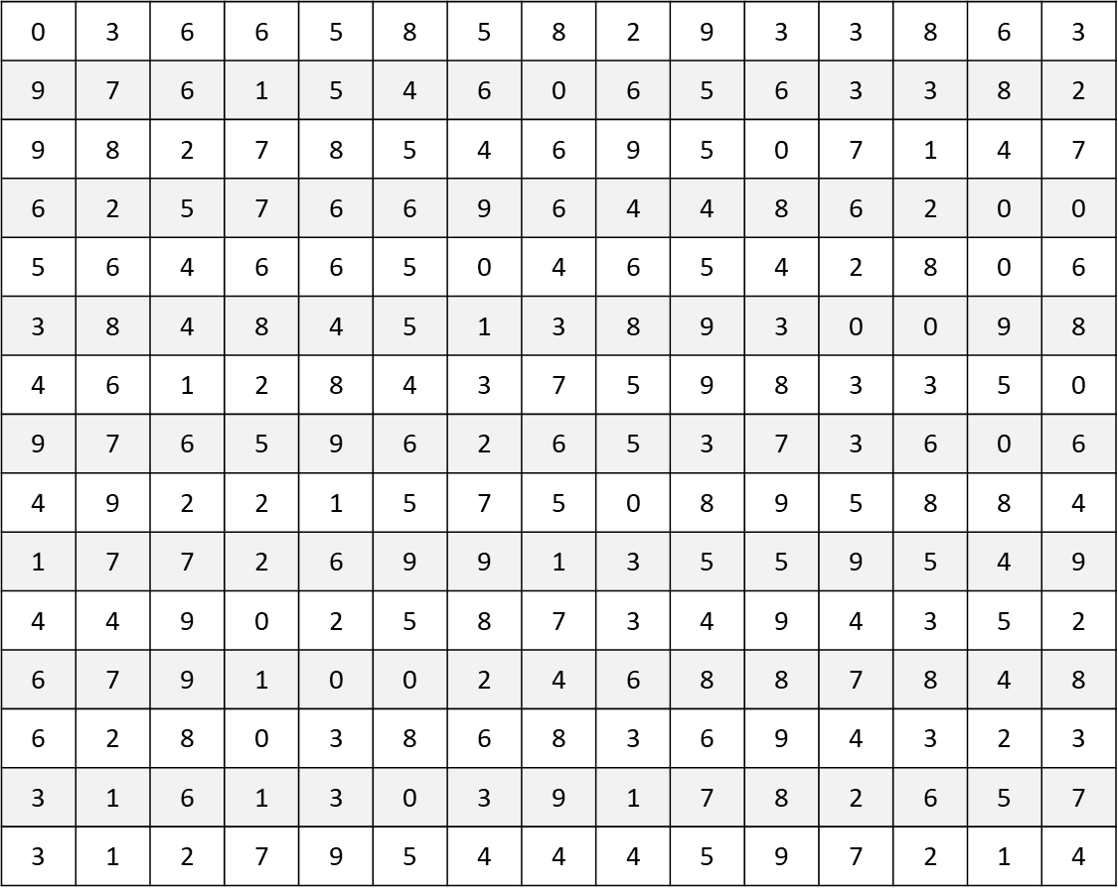
Excel version of number search for screen readers
Find the below numbers in the grid.
The numbers can be in any direction: backwards, forwards, up, down, or diagonally.
| 128036 | 438795 | 638358 |
| 132798 | 456405 | 658582 |
| 170596 | 466855 | 689972 |
| 247495 | 473829 | 782657 |
| 257669 | 488671 | 826867 |
| 274797 | 489151 | 855033 |
| 376203 | 524548 | 865664 |
| 389980 | 606563 | 868369 |
| 400950 | 608607 | 954445 |
| 414663 | 626528 | 989895 |
From www.puzzles-to-print.com