

A team of scientists wish to land a rover on Planet X, to explore and document its surface.
It takes the planet 88 Earth days to orbit the sun, and 176 Earth days to complete a rotation of its axis.
The rover they wish to use is solar powered. They will need to power-down during night on the planet.
This will mean the rover is only operational for 88 Earth days in a row, before powering down for 88 Earth days.
A researcher has suggested that with the planet being so small (3,030 miles diameter), and the day so long, it might be possible to keep the rover active permanently by having it travel around the equator at a constant speed.
This would mean the rover remains in daylight for its solar charging throughout the mission and would never need powering-down.
How fast would the rover need to travel?
Speed = distance ÷ time
The distance is the circumference of the planet
Circumference = π x diameter
Time = 176 Earth days
speed = distance (miles) ÷ time (hours)
speed = (π x 3030) ÷ (176 x 24)
using π = 3.14
speed = 9514.2 ÷ 4224
speed = 2.25 mph (to 2 d.p)
Ffion has £4.40 in 2p and 5p coins.
She has 100 coins altogether.
How many of each type of coin does she have?
Using x = number of 2p coins and y = number of 5p coins
We can write these two equations:
x + y = 100
2x + 5y = 440
⓵ x + y = 100
⓶ 2x + 5y = 440
5 x ⓵ 5x + 5y = 500
Subtract ⓶
5x + 5y = 500
-2x + 5y = 440
3x + 0 = 60
So x = 20
sub x = 20 into ⓵
20 + y = 100
So y = 80
Ffion has 20 2p coins and 80 5p coins
To complete this puzzle you need to fill all the empty squares with the numbers 1-4.
Like a sudoku, no number can appear more than once in the same row or column.
The main difference is that there are smaller blocks present which are labelled with the result of the numbers inside using the operation given.
For example: A block of 4 numbers is labelled as 10+, this means all four numbers in it must add up to 10; A block of two numbers labelled as 8x means the numbers must equal 8 when multiplied together.
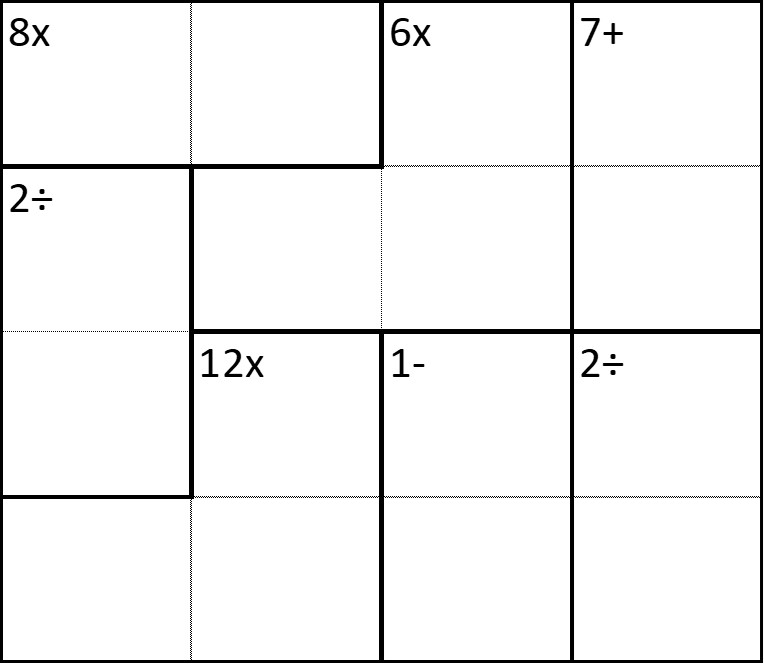
Start by look in the top left corner of the puzzle.
The two numbers in the block labelled 8x must be 2 and 4.
This means that the 2÷ block beneath must be 2 and 1 because it cannot be 4 and 2 without repeating a number in a column.
For Tomos's birthday the family unpack their two paddling pools.
Tomos's paddling pool is cylindrical. It is 60cm deep and has a diameter of 1.8m.
Steve's paddling pool is a cuboid 2m wide, 1.3m long and 80cm deep.
If Tomos fills his paddling pool completely, yet Steve only three-quarter fills his, which has the most water and by how much?
The volume of a cylinder is calculated using the equation:
volume = (π x radius2) x height
The volume of a cuboid is calculated using the equation:
volume = width x length x height
volume of a cylinder = (π x radius2) x height
radius = diameter ÷ 2
volume of Tomos's paddling pool = (π x (0.9m)2) x 0.6m
volume of Tomos's paddling pool = (π x 0.81) x 0.6
if we take π = 3.14
volume of Tomos's paddling pool = 1.53m3 (to 2 d.p)
volume of a cuboid = width x length x height
height = 3⁄4 of 80cm = 60cm or 0.6m
volume of Steve's paddling pool = 2m x 1.3m x 0.6m = 1.56m3
Steve's paddling pool has approximately 0.3m3 more water in it than Tomos's
For this exercise you will require a strip of paper (2cm x 20cm works well), and some sellotape or a glue stick.
You do not need to cut or tear the paper at all.
You will only need to stick the ends together.
There is a twist to this challenge.
Before sticking the ends together in a loop, put a single twist into the paper.
This is called a Möbius Strip.
To test, try to run your finger or pencil along the outside edge and you should find yourself also travelling the inside edge without lifting your finger/pencil

By David Benbennick - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=50359