Walking through paper
For this exercise you will need a sheet of A4 paper and a pair of scissors.
Challenge: Cut a hole in the A4 piece of paper that is large enough for you to step through!
A selection of mathematical puzzles, conundrums, and challenges for all ages.
Please select a suitable maximum level of difficulty for you. All puzzles come with hints, explanations, and answers.
Clicking on a button will randomly select the next puzzle for you.
If seven thousand, seven hundred and seven pounds is written as £7,707, how should thirteen thousand, thirteen hundred and thirteen pounds be written?
You will need to do a sum to get the correct answer for this.
13,000 + 1,300 + 13 = 14,313
1, 4, 7, 10, 13 ...
What are the next two numbers in this sequence?
What number comes after 40?
What is the common difference between each number?
Add 3 each time:
1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43
1, 3, 9, 27, 81 ...
What are the next two numbers in this sequence?
What number comes after 6,561?
What do you need to do to the previous number to get the next?
Multiply by 3 each time:
1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683
1, 3, 6, 10, 15 ...
What are the next two numbers in this sequence?
What number comes after 45?
Either:
or
Triangular numbers or +1, +2, +3, +4, +5 ...
1, 3, 6, 10, 15, 21, 28, 36, 45, 55
The day before yesterday Jasmin was nine years old. Next year she will be twelve. How is this possible?
There is only one day in the year where this can be possible.
It is the 1st January and Jasmin's birthday is on the 31st December. This means she was 9 on the 30th December, 10 on the 31st December, will be eleven at the end of this year and then 12 at the end of next.
For this exercise you will need a sheet of A4 paper and a pair of scissors.
Challenge: Cut a hole in the A4 piece of paper that is large enough for you to step through!
Consider how to cut the paper to make it into a long connected strip.
This is an interesting challenge that may seem impossible at first, until you start thinking of how to make a loop rather than a hole. The image below shows the cut lines for one way to complete this challenge.

The closer together the lines on your paper the larger the loop you can make. It is possible to make a loop big enough to drive a car through, using just A4 paper.
As an experiment, Fred asked rugby fans at the end of two different matches for volunteers to attempt a drop-kick goal. He wanted to see if being on a home field was advantageous. He made the below results tables to show the number of volunteers and their success at the end of each match.
Home Team Fans
| Match | Volunteers | Success Rate |
|---|---|---|
| First | 100 | 40% |
| Second | 50 | 10% |
Away Team Fans
| Match | Volunteers | Success Rate |
|---|---|---|
| First | 50 | 44% |
| Second | 100 | 12% |
Fred is happy to see that he was right, fans on their home field were better than the away fans. Why?
You will need to work out how many fans were successful for both home and away.
By looking at how many of each fan group were successful, he saw that home fans success was 45⁄150 (30%), whilst away fans success was only 34⁄150 (22.67%).
1, 8, 27, 64, 125 ...
What are the next two numbers in this sequence?
What number comes after 729?
Think about the volume of cubes.
Cubed numbers or 13, 23, 33, 43, 53...
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000
0, 1, 1, 2, 3, 5, 8 ...
What are the next two numbers in this sequence?
What number comes after 55?
This sequence involves adding 2 numbers together
The Fibonacci Sequence (add the last number numbers together for the next)
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
4, 9, 25, 49 ...
What are the next two numbers in the sequence?
What number comes after 961?
This involves squares of certain numbers
Squares of prime numbers:
4, 9, 25, 49, 121, 169, 289, 361, 529, 841, 961, 1369
Three house-mates ordered pizza. When it arrived the delivery man billed them £25. The house-mates each paid £10. The delivery man gave them five £1 coins in change. As they couldn't divide it equally, they took £1 each and tipped the delivery man £2. They then realised that they had each paid a total of £9 which meant they paid £27 for the pizza and then tipped the delivery man £2 bringing the total to £29. Where did the other £1 go?
How many times are they including the tip in their calculation?
They paid £27 for the pizza and the tip. Then they received £3 change making a total of £30. Their reasoning is flawed because they've added the tip twice but not the change value.
Imagine two bridges that are exactly alike except that every dimension of one bridge is twice as large as the other. Which of the two bridges would be stronger, or is their strength the same?
How will the volume, and therefore the mass, change?
By multiplying all dimension by two you are causing a volume and mass increase of x8. The larger bridge would therefore collapse under its own weight.
If you divide forty by a half and add ten, what is the answer?
Dividing something by a half is the same as doubling it.
Remember: Division is done before addition.
(40 ÷ ½) + 10 = 90
Ioan explained to his father that he would not be attending school anymore. He said he had been doing some figuring and found that he just didn't have the time for classes. He reasoned, "I sleep eight hours a day and that totals 2,920 hours or 122 days a year. Saturdays and Sundays add up to 104 days a year. If I allow three hours a day for meals, that comes to 45 days a year. The summer holidays add up to 60 days and if I allow just two hours a day for TV and recreation, this amounts to an additional 30 days. If I add all these days, they total 361 and that's not including Christmas, Easter and the other holiday's we get." What is the flaw in Ioan's reasoning?
Look for where times have been counted more than once.
The error in his logic is that he has counted certain activities multiple times. He didn't take into account the fact he'd already counted all meals, recreation and bed times for weekends and the summer holiday before counting them as complete days.
On clearing out her attic, Glenwyn found an old padlocked wooden crate. The lock used on it was a number combination, it needed 4 digits to open. An old, tattered piece of paper was pinned to the lid. It read:
To whomever finds this box.
I, Tobius Flint, have locked away my most treasured possession in this box. Only those that know the year of my birth shall be able to open it.
Yours Sincerely
T.Flint
30th March 1964
(-3,4)(3,-4)(-3,2)(-1,-1)(2,2)(2,4)(1,-4)(-3,-4)(3,4)(-3,0)
(1,4)(2,-4)(-2,-2)(2,-2)(-3,1)(-1,4)(0,-4)(1,-2)(2,0)(-1,0)
(-2,4)(-1,-4)(-1,2)(3,2)(-1,1)(3,0)(-3,-2)(3,-2)(1,0)(-2,2)
(0,4)(-2,-4)(-2,2)(1,2)(-3-1)(-1,-2)
(3,1)(1,-1)(-2,0)
What is the four digit number to unlock this padlock?
Rather than plotting co-ordinates on vertices, try colouring in squares for a clearer picture
By plotting the co-ordinates into squares and colouring them according to the note you should have:
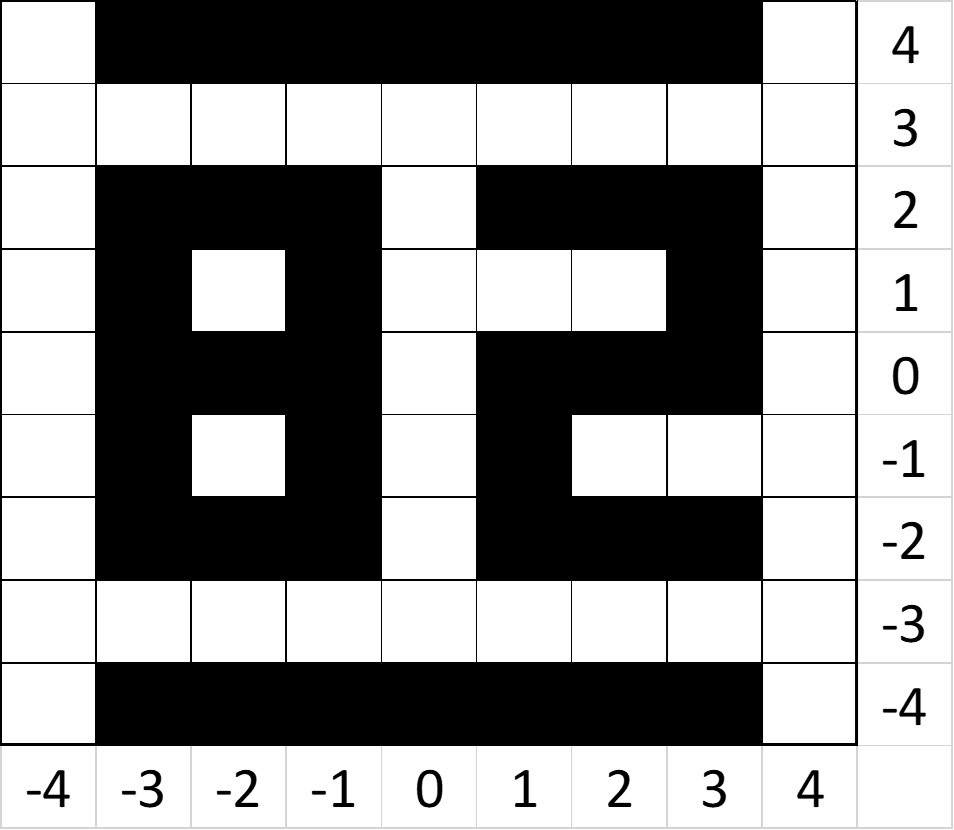
This number could either be the man's age or the last two digits of his date of birth. Using the date on the letter, both approaches will reward you with the answer: 1882.
This is a riddle believed to have been created by Albert Einstein when he was just a child. This challenge can be overcome purely by logic.
There are five neighbouring houses, painted five different colours. A person with a different nationality lives in each house. The five house owners each drink a certain type of beverage, play a certain sport, and keep a certain pet. No owners have the same pet, play the same sport, or drink the same beverage.
Who owns the fish?
You will need to use the following facts to work this out.
You will need to use this Logic Grid. If you do not know how to use a logic grid, you can visit this logic puzzle website for a tutorial
| House 1 | House 2 | House 3 | House 4 | House 5 | |
|---|---|---|---|---|---|
| Nationality | Norwegian | Danish | British | German | Swedish |
| Colour | yellow | blue | red | green | white |
| Beverage | water | tea | milk | coffee | beer |
| Sport | baseball | volleyball | football | hockey | tennis |
| Pet | cat | horse | bird | fish | dog |
A fashionable shirt is manufactured in adult and child versions, 3 different sizes (S,M,L), 10 different colours and comes with 3 different accessories.
Accessories are not necessary, but can be used together in any combination.
How many different choices of shirt and accessories are available?
Number of accessory combinations are 8 (no accessories, one accessory (3 options), two accessories (3 combinations) and all accessories)
Choose either adult or child (2 options)
Choose size (3 options)
Choose colour (10 options)
Choose accessories (8 options) (none, one of three, two of three, or all three)
So total number of combinations = 2 x 3 x 10 x 8 = 480.
This maths problem is from a Scottish Highers Exam by SQA (2015, Paper 2, Q8).
A crocodile is stalking prey located 20 metres further upstream on the opposite bank of a river.
Crocodiles travel at different speeds on land and in water.
The time taken for the crocodile to reach its prey can be minimised if it swims to a particular point, P, x metres upstream on the other side of the river as shown in the diagram.
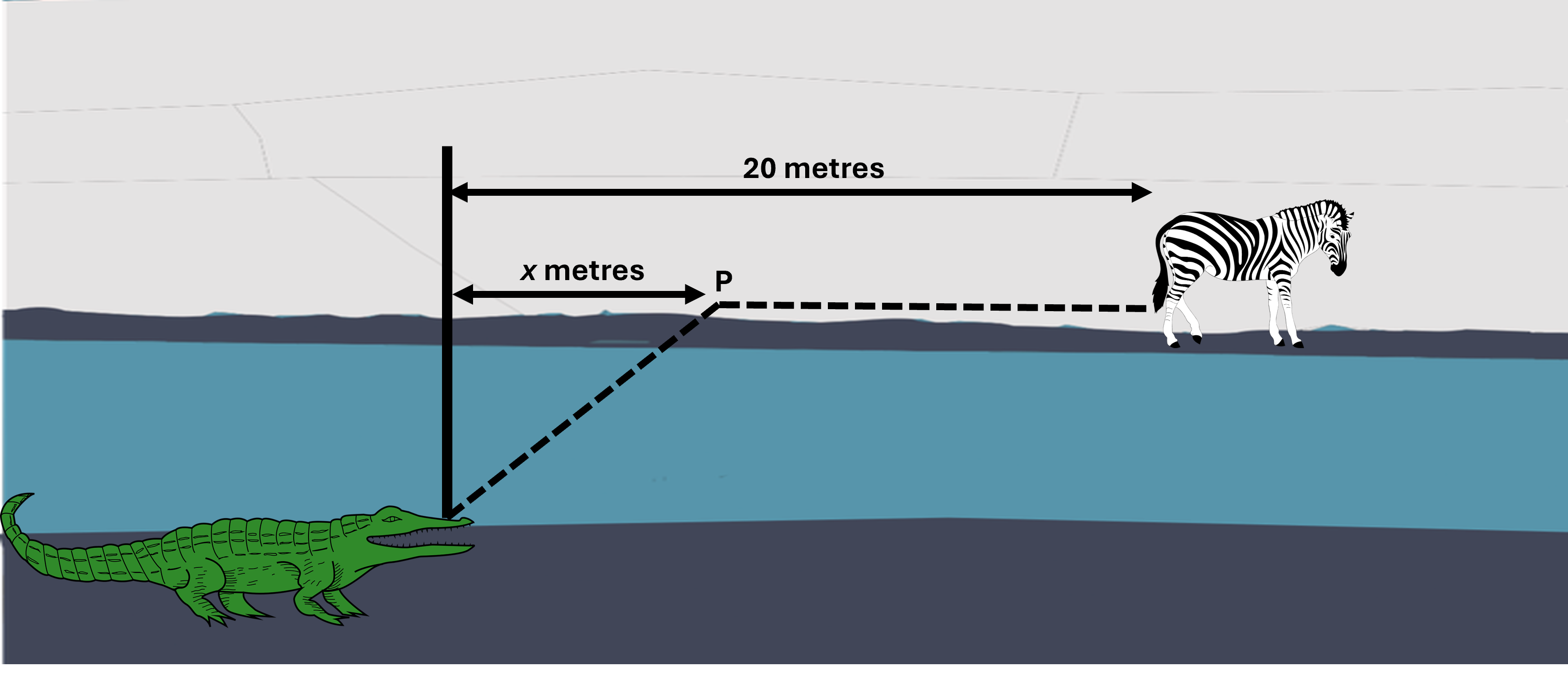
The time taken, T, measured in tenths of a second, is given by:
\[T(x) = 5\sqrt{36 + x^2} + 4(20 - x)\]
The equation gives you the width of the river, just look for the Pythagoras equation.