Cerdded trwy bapur
Bydd angen dalen o bapur A4 a siswrn arnoch chi i wneud yr ymarfer hwn.
Her: Torrwch dwll yn y darn papur A4 sy'n ddigon mawr ichi gamu drwyddo!
A selection of mathematical puzzles, conundrums, and challenges for all ages.
Please select a suitable maximum level of difficulty for you. All puzzles come with hints, explanations, and answers.
Clicking on a button will randomly select the next puzzle for you.
Os yw saith mil, saith cant a saith o bunnoedd yn cael ei ysgrifennu fel £7,707, sut byddai un deg tri mil, un deg tri cant ac un deg tri punt yn cael ei ysgrifennu?
Bydd angen i chi wneud swm.
13,000 + 1,300 + 13 = 14,313
1, 4, 7, 10, 13 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 40?
Beth yw'r gwahaniaeth cyffredin rhwng pob rhif?
Beth yw'r gwahaniaeth cyffredin rhwng pob rhif?:
1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43
1, 3, 9, 27, 81 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 6,561?
Beth sy'n rhaid i chi ei wneud i'r rhif blaenorol i gael y rhif nesaf?
Lluoswch gyda 3 bob tro:
1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683
1, 3, 6, 10, 15 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 45?
Either:
or
Rhifau trionglog neu +1, +2, +3, +4, +5 ...
1, 3, 6, 10, 15, 21, 28, 36, 45, 55
Echdoe roedd Jasmin yn naw mlwydd oed. Y flwyddyn nesaf mi fydd hi'n ddeuddeg oed. Sut mae hynny'n bosib?
Dim ond os yw ei phen-blwydd yn digwydd ar ddiwrnod penodol o'r flwyddyn y gall hyn fod yn wir.
Mae'n Ionawr 1af ac mae pen-blwydd Jasmin ar Ragfyr 31ain. Mae hyn yn golygu ei bod hi'n 9 oed ar Ragfyr 30ain, 10 oed ar Ragfyr 31ain, mi fydd yn un ar ddeg oed ddiwedd eleni ac yna'n ddeuddeg oed ddiwedd y flwyddyn nesaf.
Bydd angen dalen o bapur A4 a siswrn arnoch chi i wneud yr ymarfer hwn.
Her: Torrwch dwll yn y darn papur A4 sy'n ddigon mawr ichi gamu drwyddo!
Ystyriwch sut i dorri'r papur i'w wneud yn stribyn hir, ac wedyn torri'r twll.
Dyma her ddiddorol all ymddangos yn amhosib i ddechrau, tan i chi ddechrau meddwl sut i greu dolen yn hytrach na thwll. Mae'r llun isod yn dangos y llinellau a dorrir ar gyfer un ffordd o gwblhau'r her yma.

Po fwyaf agos at ei gilydd fydd y llinellau ar eich papur, mwyaf fydd y ddolen y gallwch ei chreu. Mae'n bosib creu dolen sy'n ddigon mawr i yrru car drwyddi trwy ddefnyddio papur A4 yn unig.
Fel arbrawf, gofynnodd Ffred i'r cefnogwyr rygbi ar ddiwedd dwy gêm wahanol am wirfoddolwyr i roi cynnig ar gic adlam. Roedd am weld a oedd bod ar gae'r tîm cartref o fantais. He made the below results tables to show the number of volunteers and their success at the end of each match.
Home Team Fans
| Gêm | Gwirfoddolwyr | Cyfradd Llwyddiant |
|---|---|---|
| Cyntaf | 100 | 40% |
| Ail | 50 | 10% |
Away Team Fans
| Gêm | Gwirfoddolwyr | Cyfradd Llwyddiant |
|---|---|---|
| Cyntaf | 50 | 44% |
| Ail | 100 | 12% |
Roedd Ffred yn hapus i gael ei brofi'n gywir, roedd y cefnogwyr ar gae'r tîm cartref yn well na'r cefnogwyr oddi cartref. Sut gall ef brofi hyn?
Bydd yn rhaid i chi weithio allan faint o gefnogwyr oedd yn llwyddiannus ar gyfer y cefnogwyr cartref a'r cefnogwyr oddi cartref.
Drwy edrych ar faint o bob grŵp cefnogwyr oedd yn llwyddiannus, gwelodd fod 45⁄150 (30%) o'r cefnogwyr cartref yn llwyddiannus, ac mai dim ond 34⁄150 (22.67%) o'r cefnogwyr oddi cartref oedd yn llwyddiannus.
1, 8, 27, 64, 125 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 729?
Think about the volume of cubes.
Rhifau ciwb neu 13, 23, 33, 43, 53...
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000
0, 1, 1, 2, 3, 5, 8 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 55?
Mae'r dilyniant hwn yn cynnwys adio 2 rif at ei gilydd
Cyfres Fibonacci (adiwch y rhifau olaf gyda'i gilydd er mwyn cael y rhif nesaf)
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
4, 9, 25, 49 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 961?
Mae'n cynnwys sgwariau rhifau penodol
Sgwariau rhifau cysefin:
4, 9, 25, 49, 121, 169, 289, 361, 529, 841, 961, 1369
Mae tri o bobl yn rhannu tŷ ac maent yn archebu pitsa. Pan gyrhaeddodd, gwnaeth y dyn dosbarthu pitsas godi £25 arnyn nhw amdano. Rhoddodd pob un o'r tri £10 iddo. Rhoddodd y dyn dosbarthu newid iddynt, sef pum darn £1. Gan nad oedden nhw'n gallu rhannu hynny'n gyfartal, fe gymerodd pawb un darn £1, gan roi'r £2 arall i'r dyn dosbarthu. Wedyn fe wnaethan nhw sylweddoli bod pob un ohonynt wedi talu £9 i gyd am y pitsa, sy'n golygu bod y cyfanswm wedi dod i £27 ac wedyn eu bod wedi rhoi tip, £2, i'r dyn dosbarthu, sy'n dod i £29 i gyd. I ble aeth y £1 arall?
Sawl gwaith maen nhw'n cynnwys y cildwrn wrth gyfrifo?
Fe wnaethant dalu £27 am y pitsa a'r tip. Yna fe gawsant newid o £3 gan wneud cyfanswm o £30. Mae eu rhesymu'n ddiffygiol am iddynt adio'r tip ddwywaith ond nid gwerth y newid.
Dychmygwch ddwy bont sydd union yr un fath ond bod pob dimensiwn un o'r pontydd ddwywaith mor fawr â'r llall. Pa un o'r ddwy bont fyddai'n gryfach, neu ai'r un yw eu cryfder?
Os ydych chi'n dyblu'r dimensiynau, beth fydd yr effaith ar y màs?
Trwy luosi pob dimensiwn â dau rydych yn cynyddu'r màs x8. Byddai'r bont fwyaf, felly yn dymchwel o dan ei phwysau ei hun.
Os ydych yn rhannu pedwar deg â hanner ac yn ychwanegu deg, beth yw'r ateb?
Bydd angen i chi gofio'r rheol arbennig ar gyfer rhannu â ffracsiynau.
Remember: Division is done before addition.
(40 ÷ ½) + 10 = 90
Eglurodd Ioan wrth ei dad na fyddai'n mynd i'r ysgol eto. Dywedodd ei fod wedi bod yn gwneud symiau ac nad oedd ganddo amser i fynd i'w ddosbarthiadau. Rhesymodd, "Rwy'n cysgu wyth awr y dydd ac mae hynny'n gyfanswm o 2,920 awr neu 122 diwrnod y flwyddyn. Mae cyfrif pob dydd Sadwrn a dydd Sul yn gyfanswm o 104 diwrnod y flwyddyn. Os ydw i'n neilltuo tair awr y dydd ar gyfer prydau bwyd, mae hynny'n 45 diwrnod y flwyddyn. Mae gwyliau'r haf yn 60 diwrnod ac os ydw i'n neilltuo dwy awr yn unig bob dydd ar gyfer teledu a hamdden, mae hynny'n ychwanegu 30 diwrnod arall. Os ydw i'n cyfrif yr holl ddyddiau hyn, mae'n dod i gyfanswm o 361 heb gynnwys y Nadolig, y Pasg a'r gwyliau eraill." Beth yw'r gwendid yn rhesymu Ioan?
Sawl gwaith y mae ef wedi cyfrif pob agwedd?
Camgymeriad rhesymeg Ioan yw ei fod wedi cyfrif rhai gweithgareddau sawl gwaith. Ni wnaeth gymryd i ystyriaeth ei fod eisoes wedi cyfrif pob pryd bwyd, amser hamdden ac amser gwely ar gyfer penwythnosau a gwyliau'r haf cyn eu cyfrif yn ddiwrnodau llawn.
Wrth glirio'r atig, daeth Glenwyn o hyd i grêt pren a chlo arno. Cyfuniad o rifau oedd y clo a ddefnyddiwyd, ac roedd angen 4 digid i'w agor. Roedd hen ddarn o bapur drylliog ar y clawr ac arno'r geiriau:
I bwy bynnag ddaw o hyd i'r blwch hwn.
Yr wyf i, Tobius Flint, wedi cloi fy nhrysor pennaf yn y blwch hwn. Dim ond y rhai sy'n gwybod blwyddyn fy ngeni fydd yn gallu ei agor.
Yn gywir
T.Flint
Mawrth 30ain 1964
(-3,4)(3,-4)(-3,2)(-1,-1)(2,2)(2,4)(1,-4)(-3,-4)(3,4)(-3,0)
(1,4)(2,-4)(-2,-2)(2,-2)(-3,1)(-1,4)(0,-4)(1,-2)(2,0)(-1,0)
(-2,4)(-1,-4)(-1,2)(3,2)(-1,1)(3,0)(-3,-2)(3,-2)(1,0)(-2,2)
(0,4)(-2,-4)(-2,2)(1,2)(-3-1)(-1,-2)
(3,1)(1,-1)(-2,0)
Beth yw'r rhif pedwar digid sy'n angenrheidiol ar gyfer agor y clo?
Defnyddiwch bapur sgwariau ac, yn hytrach na phlotio'r cyfesurynnau ar fertigau, ceisiwch liwio'r sgwariau i mewn er mwyn cael darlun cliriach
Trwy blotio'r cyfesurynnau mewn sgwariau a'u lliwio yn unol â'r nodyn, dylai fod gennych:

Gallai'r rhif hwn un ai fod yn oed y dyn neu ddau ddigid olaf ei ddyddiad geni. Trwy ddefnyddio'r dyddiad ar y llythyr, bydd y ddau ddull yn rhoi'r ateb i chi: 1882.
Mae'n debyg fod y Albert Einstein wedi creu'r pos hwn pan oedd yn blentyn. Gellir goresgyn yr her yma trwy ddefnyddio rhesymeg yn unig.
Mae pum tŷ drws nesaf i'w gilydd, sydd wedi'u paentio'n bum gwahanol liw. Mae person o genedl wahanol yn byw ym mhob tŷ. Mae pum perchennog y tai yn yfed gwahanol fath o ddiod, yn chwarae math penodol o chwaraeon, ac yn cadw anifail anwes penodol. Nid oes gan yr un perchennog yr un anifail anwes, nac yn chwarae'r un math o chwaraeon, nac yn yfed yr un diod.
Pwy biau'r pysgodyn?
Bydd yn rhaid i chi ddefnyddio'r ffeithiau isod i ganfod yr ateb.
Bydd yn rhaid i chi ddefnyddio'r Grid Rhesymu (yn Saesneg). Os nad ydych yn gwybod sut i ddefnyddio grid rhesymu, gallwch wylio tiwtorial ar y wefan posau rhesymu hon.
| Tŷ 1 | Tŷ 2 | Tŷ 3 | Tŷ 4 | Tŷ 5 | |
|---|---|---|---|---|---|
| Cenedligrwydd | Norwyaidd | Danaidd | Prydeinig | Almaenaidd | Swedaidd |
| Lliw | melyn | glas | coch | gwyrdd | gwyn |
| Diod | dŵr | te | llaeth | coffi | cwrw |
| Chwaraeon | pêl fas | pêl foli | pêl droed | hoci | tenis |
| Anifail Anwes | cath | ceffyl | aderyn | pysgodyn | ci |
Caiff crys ffasiynol ei gynhyrchu mewn fersiynau i oedolion a phlant mewn 3 maint gwahanol (bach, canolig a mawr), mewn 10 lliw gwahanol ac mae ganddo 3 o ategolion gwahanol.
Nid yw'r ategolion yn angenrheidiol ond gellir eu defnyddio gyda'i gilydd mewn unrhyw gyfuniad.
Faint o wahanol ddewisiadau o grys ac ategolion sydd ar gael?
Y nifer o gyfuniadau o ategolion yw 8 (dim ategolyn, un ategolyn (3 opsiwn), dau ategolyn (3 chyfuniad) a'r ategolion i gyd)
Dewiswch un ai oedolyn neu blentyn (2 ddewis)
Dewiswch faint (3 dewis)
Dewiswch liw (10 dewis)
Dewiswch ategolion (8 dewis) (dim, un o dri, dau o dri, neu'r tri)
Felly, cyfanswm y cyfuniadau yw = 2 x 3 x 10 x 8 = 480.
Daw'r broblem fathemateg hon o Arholiad Uwch yr Alban gan Awdurdod Cymwysterau'r Alban (2015, Papur 2, Cwestiwn 8).
Mae crocodeil yn hela ysglyfaeth sydd 20 metr i fyny'r afon ar lan arall afon.
Mae crocodeilod yn teithio ar wahanol gyflymdra ar dir ac yn y dŵr.
Gellir lleihau'r amser mae'n ei gymryd i'r crocodeil gyrraedd ei ysglyfaeth os yw'n nofio at fan penodol, P, x metrau i fyny'r afon ar ochr arall yr afon fel sy'n cael ei ddangos yn y diagram.
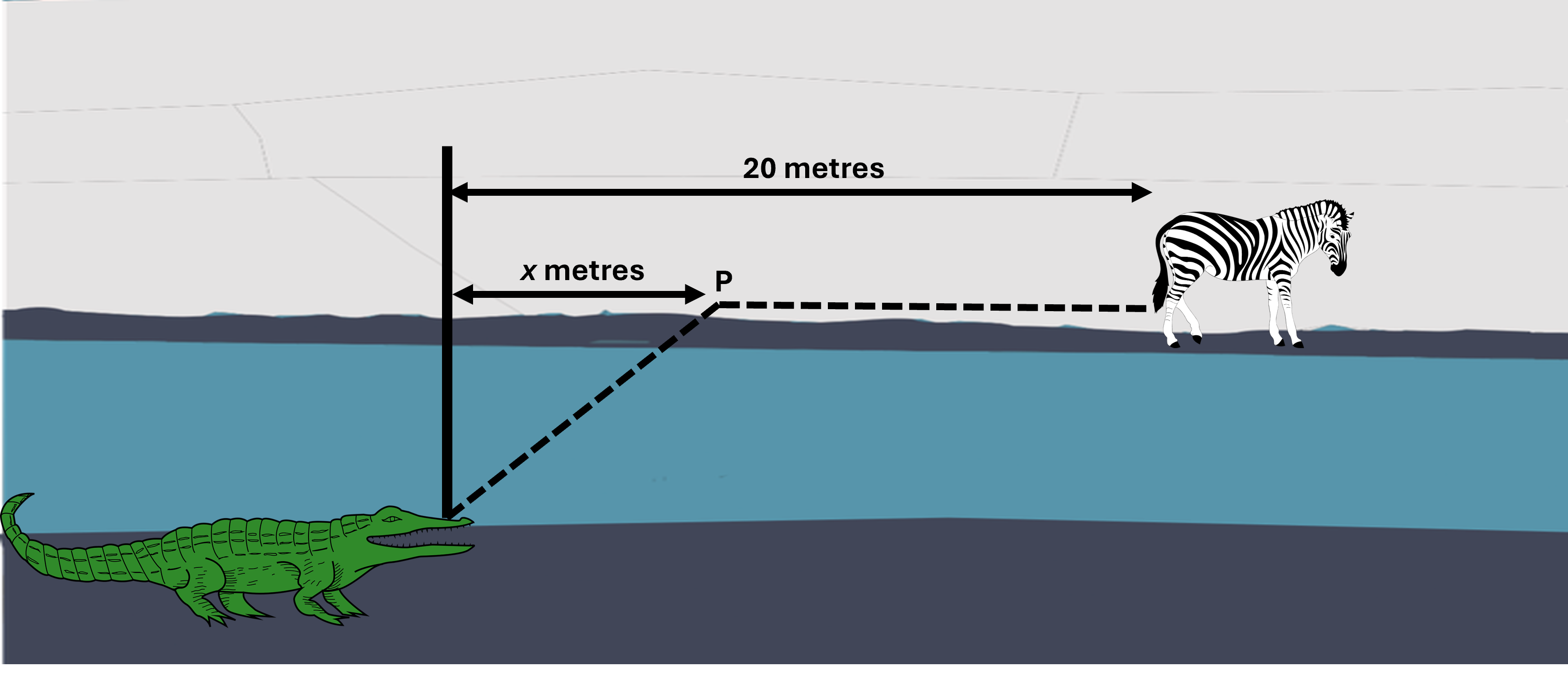
Mae'r amser mae'n ei gymryd, T, yn cael ei fesur mewn degfed ran o eiliad, ac yn cael ei roi trwy
\[T(x) = 5\sqrt{36 + x^2} + 4(20 - x)\]
Mae'r hafaliad yn rhoi lled yr afon i chi, chwiliwch am hafaliad Pythagoras.